Understanding the Time Complexity

This article is based on the Time Complexity concept. If you have done or doing computer science you must have come across this topic. Many interviewers ask questions based on this topic. for the programmer, it is necessary to make sure that the code written by him has the lowest running time and efficient

Why do we need to understand time complexity?
What is Time Complexity?
Different Type of Time Complexity
Asymptotic notations.
How to find time Complexity?
Some Examples

Why do we need to understand time complexity?

Suppose you and your friend are taking part in one competition and you both want to implement sorting functionality for school students by their marks. As you both don't have an idea about time complexity it was decided that whoever's code will give the first result will be the winner. Now, you are using Python and your friend uses C/C++. As we all know C/C++ is faster than Python, your solution was taking 5.5 sec and your friend's solution was taking 5.1 sec.

Now suppose your friend has a Macbook or laptop with good hardware and you do not have that sufficient system. So, Even if your solution is better than your friend's, your friend will be a winner as his code will give faster output.

So you and your friend came to know that time taken by solution is depends on so many parameters, so to find proper efficiency of the algorithm we need some other parameter which is a number of operation performed by an algorithm to solve the problem of size N.

As we all know modern CPU can perform up to 10 million instructions per second so if we measure how many operations our algorithm will take to solve the problem then we can do an analysis on the running time of an algorithm

What is Time Complexity?

So by definition, Time complexity is the number of steps(operation) taken by the algorithm to run, as a function of the size of the input.

Different Type of Time Complexity

Constant Time - O(1)
Linear Time - O(N)
Logarithmic time - O(logN)
Quadratic time – O (N^2)
Cubic time – O (N^3)

Constant Time: As the name suggests it takes a constant number of operations to perform tasks no matter what is the size of the input. Suppose we do 2 + 3 or 2000 + 3000 it will always take a constant number of operations. it is not dependant on data.
Linear Time: An algorithm is said to have a linear time complexity when the running time increases linearly with the length of the input. When the function involves checking all the values in input data, such function has Time complexity with this order O(n).
Logarithmic time - O(logN): An algorithm is said to have a logarithmic time complexity where the running time increases logarithmically with the length of the input
Quadratic time – O (N^2): An algorithm is said to have a non – linear time complexity where the running time increases non-linearly (n^2) with the length of the input

Refer to the below graph as it will give an idea of how the number of operations increases based on size of input for different time complexities.

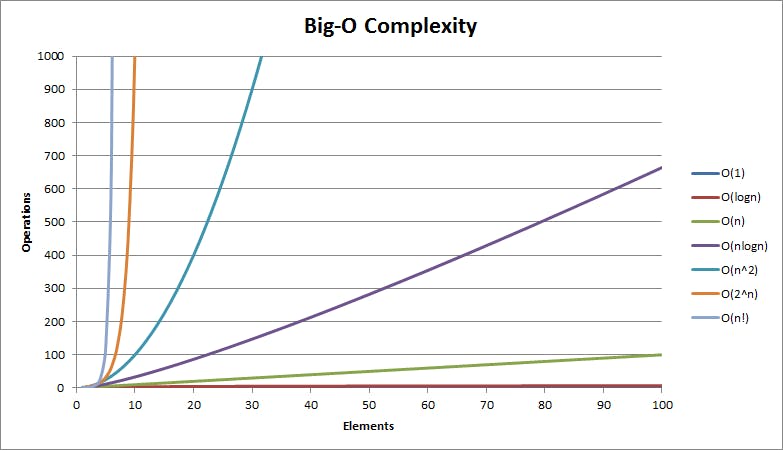Image Source: HackerEarth

Asymptotic notations.

The Big-O notation: This gives the tight upper bound of the given function. It describes the worst-case running time of a program. We compute the Big-O of an algorithm by counting how many iterations an algorithm will take in the worst-case scenario with an input of N. For example, O(log n) describes the Big-O of a binary search algorithm. For example, if the algorithm is taking f(n) = 2n^2 + 5n number of steps we will call its time complexity is O(n^2). because as the value of n increases the rate of growth at lower values of n is not important. So, when we say that an algorithm X is asymptotically more efficient than Y it means X will always be a better choice for large inputs
The Big-Ω notation: It is often used to describe best case time complexity, by choosing the lowest order of the polynomial function. So we compute how many operation algorithms will take in the best-case scenario. Bubble sort will take n operation in best case when the array is already sorted so we can say that Big Omega for Bubble sort is Ω(n)
The Theta-Θ notation: The average running time of the algorithm will be always between Big-O(upper bound) and Big-Ω(lower bound). If the Big-O and Big-Ω give the same result then Θ notation will help. We generally focus on worst-case time complexity (Big-O) because knowing the best case time complexity has no practical importance so we will use Big-O notation for every algorithm.

How to find time complexity?

print elements of a 1D array

# this will be executed N times(length of array)
for item in range(0, len(array): 
     # internal function call to print element
     print(array[item]) 

suppose print statement takes 3 CPU
cycles and it will be executed N time 
so total number of operations are 
TC = 3 * N 
and we are interested in only asymptotic notation so we can say that it is
TC = O(N) (Big O of N)

Print elements of a 2D array

for each row in matrix:
    for each column in row:
        print(matrix[row][column])

If we have N rows and N columns print statement 
will be executed N * N times.

So, TC = 3 * N * N
TC = O(N^2)

To find the time complexity of any code we need to find the total number of operations it will take with respect to the size of the input. Let's look at some examples.

Example Problems

Example 1: Better for loop

We have four different functions with a single for loop and the same set of expressions in for loop.

  A) for(i = 0; i < n; i++)

  B) for(i = 0; i < n; i += 2)

  C) for(i = 1; i < n; i *= 2)

  D) for(i = n; i > -1; i /= 2)

Which one will be faster?

Answer: C 

The time complexity of the first for loop is O(n). 

The time complexity of the second for loop is O(n/2), equivalent to O(n) in asymptotic analysis. 

The time complexity of the third for loop is O(logn) as we double value of i in every step. 

The fourth for loop doesn't terminate and is an infinite loop.

Example 2: What is the Time Complexity of the following code?

int i, j, k = 0;
  for (i  = n/2; i <= n; i++) {
      for (j = 2; j <= n; j = j * 2) {
          k = k + n/2;
      }
  }

Now, let's just assume n = 8 for now. We will try to see, the values of j corresponding to each i.

i = 4, j = 2, 4, 8

i = 5, j = 2, 4, 8

i = 6, j = 2, 4, 8

i = 7, j = 2, 4, 8

i = 8, j = 2, 4, 8

If you notice, j keeps doubling till it is less than or equal to n. The number of times, you can double a number till it is less than n would be log(n).

Let's take more examples here to convince ourselves.

n = 16, j = 2, 4, 8, 16 n = 32, j = 2, 4, 8, 16, 32

So, j would run for O(log n) steps. i run for n/2 steps.

So, total steps = O (n/ 2 * log (n)) = O(n logn)

Example 3: What is the time complexity of the following code?

int count = 0;
 for (int i = N; i > 0; i /= 2) {
       for (int j = 0; j < i; j++) {
          count += 1;
        }
 }

In the first iteration, the j loop runs N times.

In the second iteration, the j loop runs N / 2 times. 

In the ith iteration, the j loop runs N / 2^i times. 


So, the total number of runs of loop = N + N / 2 + N / 4 + ... 1 

= N * ( 1 + 1/2 + 1/4 + 1/8 + ... ) 
< 2 * N
= O(N)

Example 4: What is the time complexity of the following code?

int j = 0;
for(i = 0; i < n; ++i) {
    while(j < n && arr[i] < arr[j]) {
    j++;
    }
}

A) O(N^2)
B) O(N * sqrt(N)
C) O(N)
D) O(logN)

Example 5: Find the time Complexity of the following code?

int a = 0, b = 0;    
for (i = 0; i < N; i++) {
    for (j = 0; j < N; j++) {
        a = a + j;
    }
}
for (k = 0; k < N; k++) {
    b = b + k;
} 

A) O(N^2)
B) O(N^3)
C) O(N^2 + N)
D) O(N)

Example 4 and 5 try by yourself and add your answer in a comment. Happy Learning!!!